Let
 be the desired speed. Then, from the relativistic velocity addition formula, the speed of one space ship as measured by the other is be the desired speed. Then, from the relativistic velocity addition formula, the speed of one space ship as measured by the other is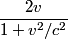 The factor by which the meterstick will be contracted is 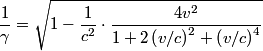 From the problem statement we know that this factor is 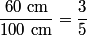 So, 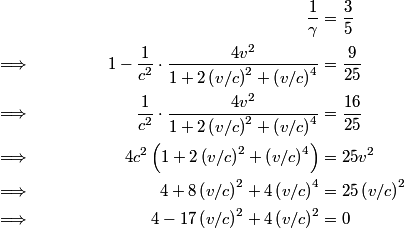 We can now apply the quadratic formula to find that 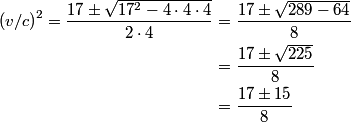 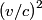 must be less than must be less than 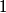 , so we take the minus sign. This gives , so we take the minus sign. This gives 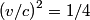 and and 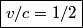 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |